KBGAN模型¹

Novelty

• 首次使用生成对抗网路的思想，全篇关注负样本的生成质量问题
• 采用生成对抗网络，采用概率模型作为生成器，采用距离模型作为鉴别器，训练鉴别器
• 使用强化学习的策略梯度方法来训练生成器

问题和动机

• 过去知识图谱嵌入领域的负采样仅仅根据概率来采样有以下两个问题
  • 假负样本问题，有可能会有正确样本被当成负样本来采样
  • 低质量负样本问题，会产生一些质量很低的，对训练意义不大的样本(很容易与正样本区分开的样本，对训练贡献很小)
• 收到对抗生成网络思想的影响，本文采用生成器来生成高质量负样本，采用鉴别器来计算嵌入
  • 生成器使用基于概率的log-loss损失
  • 鉴别器使用基于距离的margin-loss损失
  • 由于存在离散的生成过程，因此不能使用基于梯度的方法进行优化，本文采用强化学习中的方差减少方法来进行优化。

相关工作

• GAN最早用于生成图像
  • 生成器接受噪声输入并输出图像
  • 鉴别器是一种分类器，将图像分类为真和假。
  • 训练GAN时，生成器试图生成真实图像来欺骗鉴别器，鉴别器试图将其与真是图像区分开。
  • GAN还能够生成满足特定要求的样本
• 用于自然语言处理
  • 梯度传播不适用于离散采样的步骤，因此不能使用原始GAN来生成离散样本，如自然语言句子或三元组
  • SEQGAN使用强化学习来解决离散问题，使用了策略梯度和其他技巧来训练生成器。
• 鉴别器不一定是分类器。后来很多方法使用回归器作为鉴别器。

过去的解决方法

• 过去采用随机替换来生成负样本，但这样容易产生低质量的样本
• 对于log-softmax损失函数而言，通常会为一个正样本产生很多个负样本，因此总有高质量的负样本可以使用，因此低质量样本的影响不大

论文²(ComplEx)研究表明，当采用100：1的负/正比例会使得效果更佳

• 但对于margin-loss而言，正负样本通常为1:1，因此低质量负样本会影响训练

idea

• 采用一个softmax概率的生成器(这是因为softmax给出的是一组三元组的概率分布，这是生成器从中采样所必须的东西)，来生成高质量的负样本。
• 采用一个marginal损失函数来构造鉴别器，这类损失可以从高质量的负样本中受益更多。
• 本模型的最终目标是生成一个好的鉴别器，而GAN的目标是训练一个好的生成器
  • 鉴别器应该为高质量的负样本分配较小的距离
  • 生成器的目标是最小化鉴别器中为生成三元组给出的距离
  • 鉴别器的目标是最小化正三元组和负三元组之间的边际损失。
  • 生成器和鉴别器会针对各自的目标交替训练

模型

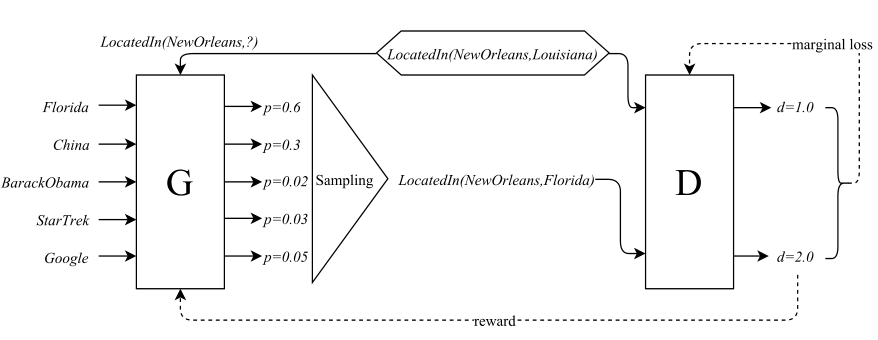
• 假设给定正三元组$(h,r,t)$，生成器给出的负三元组的概率分布为$p_G(h^\prime ,r , t^\prime | h,r,t)$，并通过该分布生成负样本$(h^\prime,r,t^\prime)$
• 鉴别器的得分函数为$f_D(h,r,t)$

生成器

• 生成器中的采样概率为$Neg(h,r,t)\subset\{(h^\prime,r,t)|h^\prime\in\mathcal{E}\}\cup\{(h,r,t^\prime)|t^\prime\in\mathcal{E}\}$ \begin{align*} p_G(h^\prime,r,t^\prime|h,r,t)=\frac{\exp f_G(h^\prime,r,t^\prime)}{\sum\exp f_G(h^\ast,r,t^\ast)} \\ (h^\ast,r,t^\ast)\in Neg(h,r,t) \end{align*}

理想情况下，$Neg(h,r,t)$应该包含所有的负样本，然而，知识图通常是高度不完整的，因此“最难”的负三元组很可能是假阴性（真实事实）。为了解决这个问题，通过从E中均匀采样Ns实体（与所有可能的负样本相比，这是一个很小的数字）来代替h或t来生成Neg（h，r，t）。因为在现实知识图中，真否定通常远远大于假否定，这样的集合不太可能包含任何假否定，生成器选择的负片很可能是真负样本。使用较小的$Neg(h,r,t)$也可以显著降低计算复杂性。

同时采用伯努利负采样的策略，以更大的概率来替换1对N和N对1中1的那端。

• 生成器的目标可表述为，最大化以下负距离的期望值 \begin{align*} R_G&=\sum_{(h,r,t)\in\mathcal{T}}\mathbb{E}[-f_D(h^\prime,r,t^\prime)] \\ &(h^\prime,r,t^\prime)\sim p_G(h^\prime,r,t^\prime|h,r,t) \end{align*}
• 此生成器有一个离散采样的步骤，因此无法直接用简单的微分求出梯度
• 采用策略梯度理论来生成上述公式的梯度 \begin{align*} \nabla_G R_G&=\sum_{(h,r,t)\in T}E_{(h^\prime,r,t^\prime)\sim p_G(h^\prime,r,t^\prime|h,r,t)} \\ &[-f_D(h^\prime,r,t^\prime)\nabla_G \log p_G(h^\prime,r,t^\prime|h,r,t)] \\ &\simeq \sum_{(h,r,t)\in\mathcal{T}}\frac{1}{N}\sum_{(h_i^\prime,r,t_i^\prime)\sim p_G(h^\prime,r,t^\prime|h,r,t), i=1\dots N} \\ &[-f_D(h^\prime,r,t^\prime)\nabla_G \log p_G(h^\prime,r,t^\prime|h,r,t)] \end{align*}

鉴别器

• 鉴别器的目标可表述为最小化如下损失函数 \begin{align*} L_D&=\sum_{(h,r,t)\in\mathcal{T}}[f_D(h,r,t)-f_D(h^\prime,r,t^\prime)+\gamma]_+ \\ &(h^\prime,r,t^\prime)\sim p_G(h^\prime,r,t^\prime|h,r,t) \end{align*}

强化学习的角度

• 生成器可以看作一个agent，通过执行操作与环境交互，通过最大化环境的响应回报来改进自身
• 鉴别器可以看作environment
• 具体而言$(h,r,t)$为状态，$p_G(h^\prime,r,t^\prime|h,r,t)$为策略，$(h^\prime,r,t^\prime)$为行动，$-f_D(h^\prime,r,t^\prime)$为汇报。
• 在典型的强化学习中，动作的每个操作都要改变状态，知道达到特定状态或者操作数达到限制。但本文中的方法不改变状态。因此每个epoch只包含一个行动。
• 在强化学习中，为了减少强化算法的方差，通常会在奖励中减去一个baseline，在本文中，我们将$-f_D(h^\prime,r,t^\prime)$替换为$-f_D(h^\prime,r,t^\prime)-b(h,r,t)$，为了不引入别的参数，设b为$b=\sum_{(h,r,t)\in\mathcal{T}}\mathbb{E}_{(h^\prime,r,t^\prime)\sim p_G(h^\prime,r,t^\prime|h,r,t)}[-f_D(h^\prime,r,t^\prime)]$

算法

实验

• 为了验证框架的可行性，本论文选择了不同的生成器和鉴别器，并验证了所有的可能组合
  • 生成器选择了两个基于概率的模型DISTMULT和CompLEx
  • 鉴别器选择了两个经典的基于翻译的模型TransE和TransR
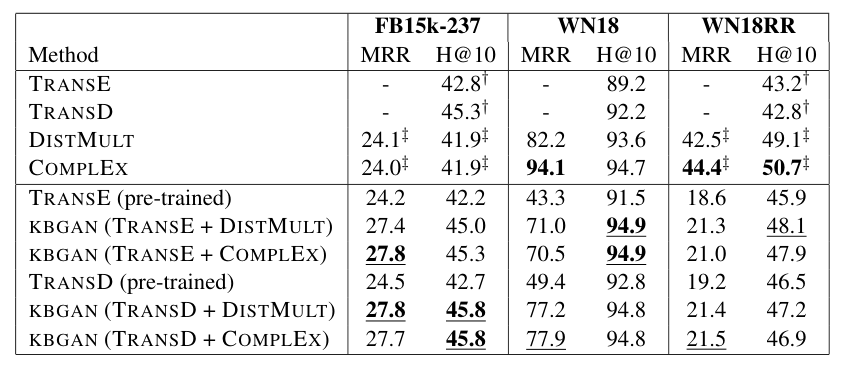
• 选择了FB15K-237和WN18以及WN8RR三个数据集来验证性能，结果如下 生成器的选择(DISTMULT或者CompLEx)不会显著影响实验结果，KGGAN框架可以提升Trans系列模型的性能
• 未来可以使用更先进的生成器或者鉴别器来优化模型性能
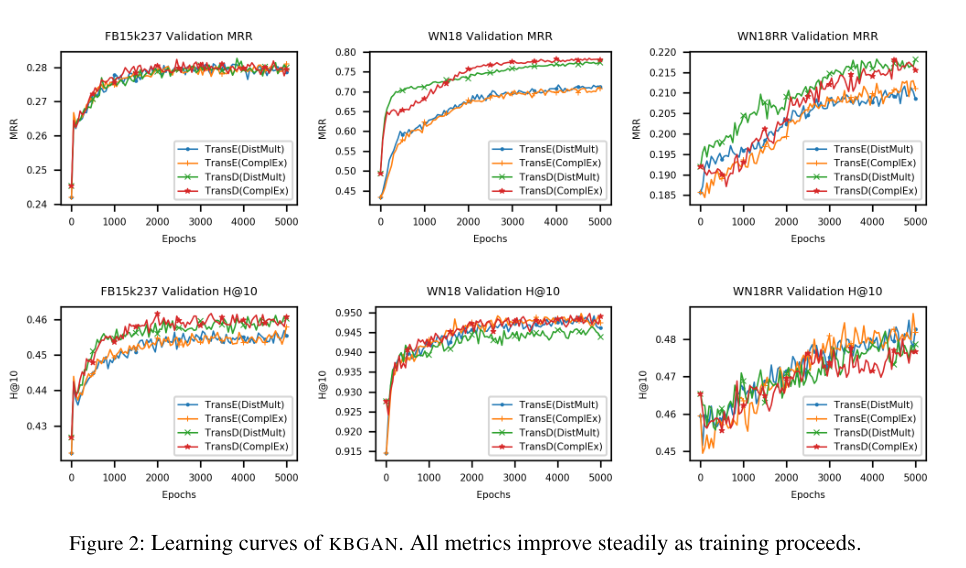
• 该模型在训练过程中性能始终处于上升状况，如下图所示