PairRE
Contents
PairRE
Novelty
- 既考虑了复杂关系建模的问题,又考虑了多种模式的关系
- 通过修改RotatE的公式,将关系参数改为头尾两个,从而可以对复杂关系进行建模(RotatE本身就可以对多种模式关系建模)
根据本文分析,RotatE本身可以对N-1关系建模,但是不能对1-N和N-N关系建模
问题和动机
KGE模型中存在两个 广泛研究的问题
- 对复杂关系进行合适建模,如N-1,1-N以及N-N的关系
- 对不同模式的关系类型进行建模,主要包括,对称/反对称,逆和合成关系。
- 对称和反对称关系
$r(x,y) \Rightarrow r(y,x) $ and $r(x,y) \Rightarrow \lnot r(y,x)$
- 逆关系
$r_2(x,y) \Rightarrow r_1(y,x)$
- 组合关系
$r_1(x,y) \land r_2(y,z) \Rightarrow r_3(x,z)$
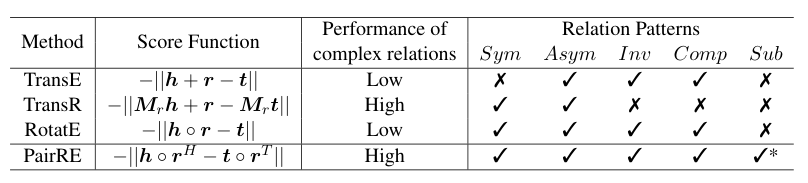
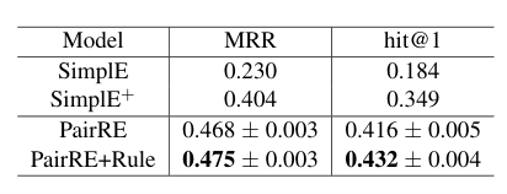
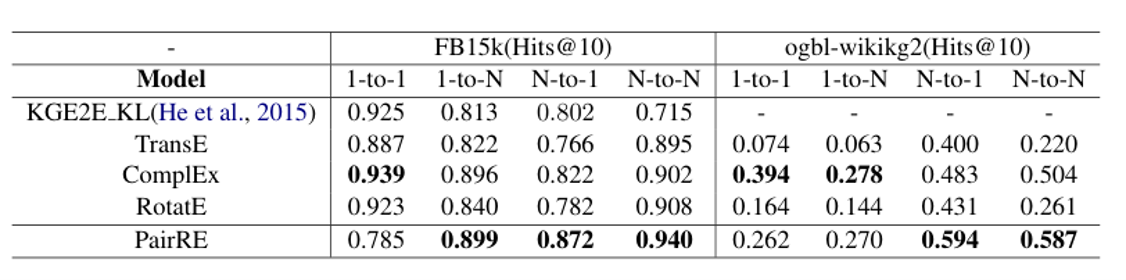
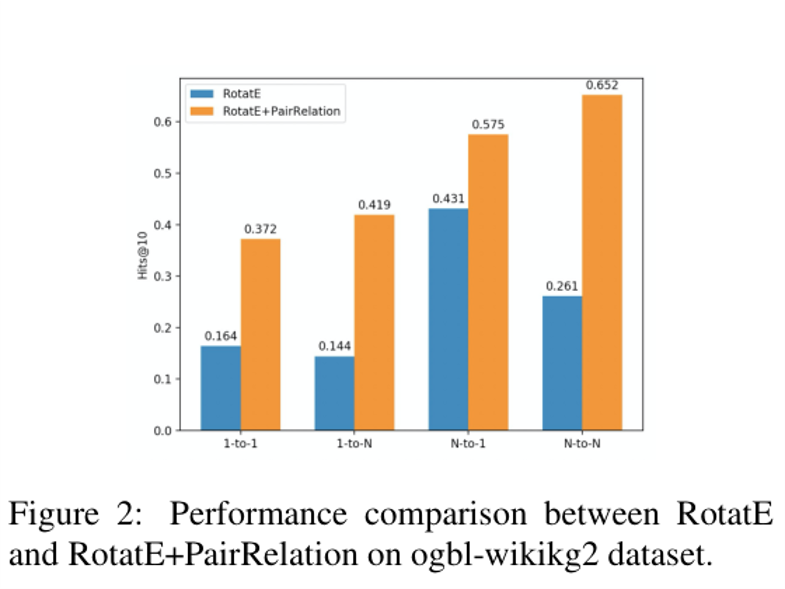
- 现有的方法并不能同时很好的解决这两种问题,如下图所示
- TransH,TransR等模型专注于解决复杂关系建模,不能对不同模式的关系建模
- RotatE可以对多种模式的关系进行建模,但复杂关系表达能力较弱
过去的解决方法
- 距离模型难以对不同模式的关系建模
- TransE将关系解释为平移向量,效率较高,难以建模对称关系,假如某个关系对称,则该关系r的嵌入向量只能为0。同时难以建模复杂关系
- TransH,TransR等模型改进了TransE难以建模复杂关系的缺点,但通常用的方法都是将实体投影到关系特定的超平面中,由于投影参数的问题,难以建模逆和合成关系。
- RotatE虽然可以对各种模式的关系进行建模,但复杂关系表现能力弱
- 语义匹配模型,如RESCAL,DisMult,HoIE,ComplEx,QuatE等模型都无法表达组合关系,而且只有嵌入维度满足大于N/32时1,才可以完全表达(N是数据集中的实体数)
- 其他神经网络模型是黑盒,难以分析

idea
- 将关系表示用两个成对的矩阵表示,分别与头尾实体做哈德曼乘积来对复杂问题进行建模
- 采用两个成对的矩阵,并采用哈德曼积,可以有效的对多种模式的关系进行建模
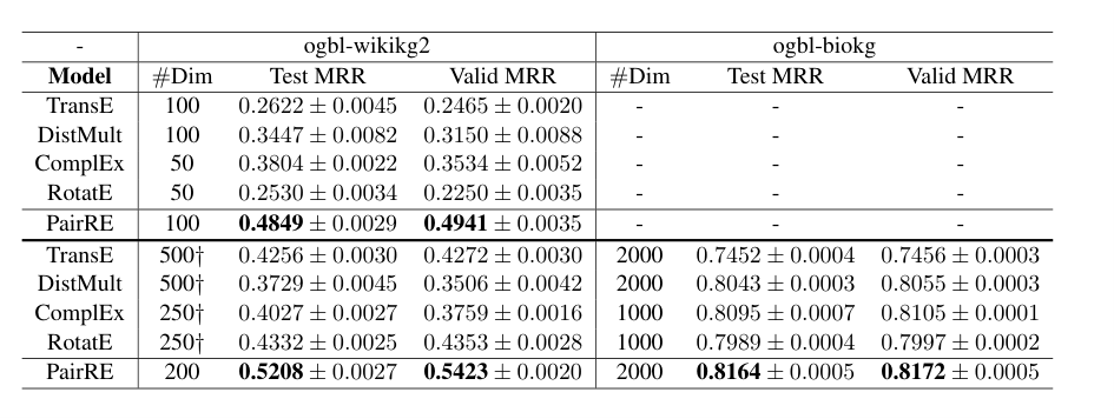
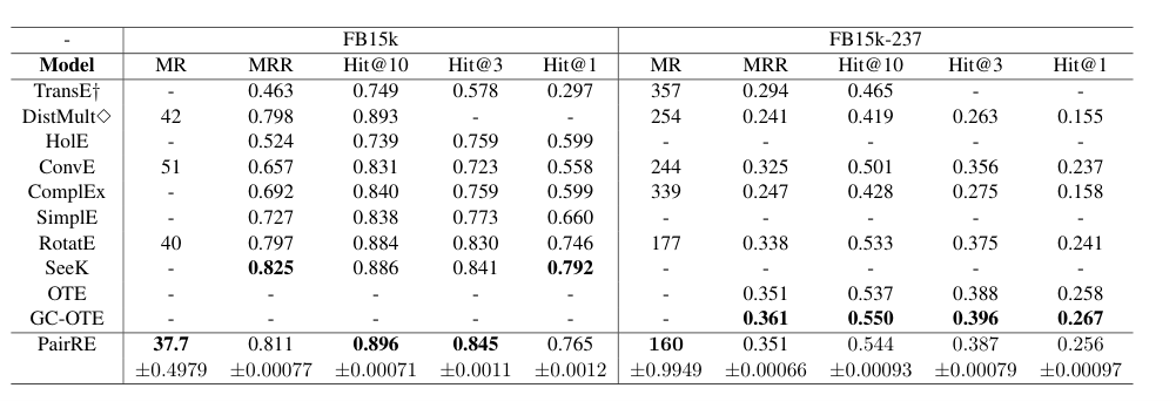
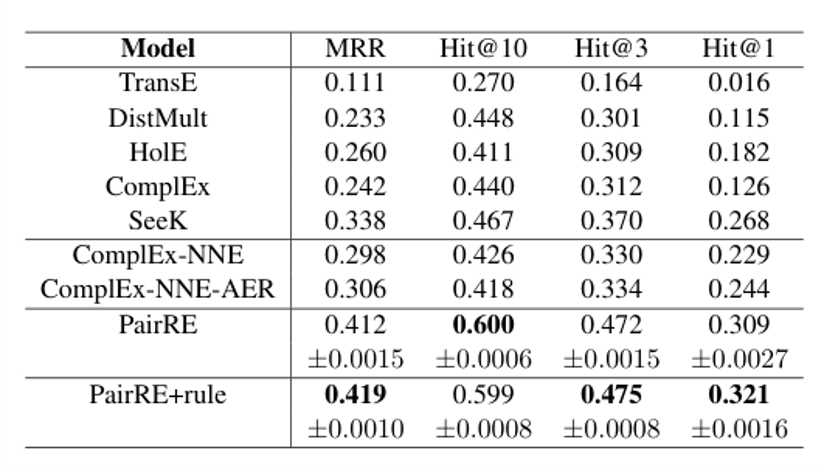
- 采用与距离模型相同的得分函数,并采用RotatE的自对抗负采样损失进行训练
- 得分函数如下 $$f_r(h,t) = -||h \circ r^H - t \circ r^T ||$$
- 损失函数如下 \begin{align*} p((h^\prime_i,r,t^\prime_i)|\{h_i,r_i,t_i\}) &= \frac{\exp f_r(h^\prime_i,t^\prime_i)}{\sum_i \exp \alpha f_r(h^\prime_j,t^\prime_j)} \\ L = &-log\sigma (\gamma - f_r(h,t)) \\ &-\sum_{i=1}^{n}p(h^\prime_i,r,t^\prime_i)log\sigma(f_r(h^\prime_i,t^\prime_i) - \gamma) \end{align*}
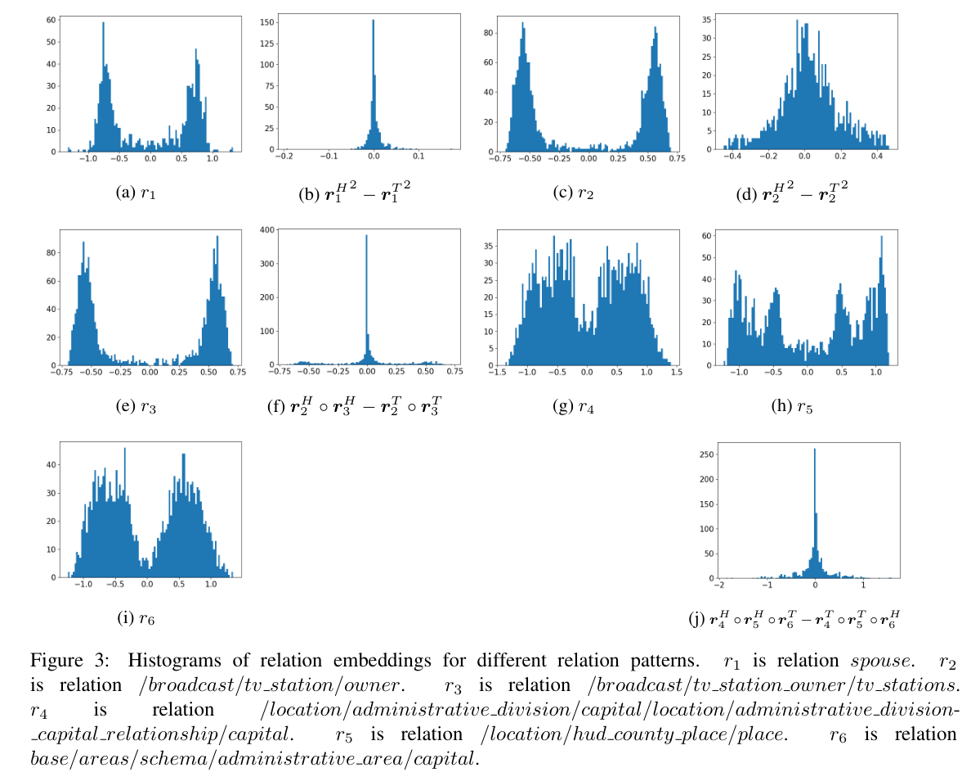
对于多种模式可表达性的证明
- 对称关系 $$ e_1 \circ r_1^H = e_2 \circ r_1^T \land e_2 \circ r_1^H = e_1 \circ r_1^T \\ \Rightarrow r_1^H = r_1^T $$
- 逆关系 $$ e_1 \circ r_1^H = e_2 \circ r_1^T \land e_2 \circ r_2^H = e_1 \circ r_2^T \\ \Rightarrow r_1^H \circ r_2^H = r_1^T \circ r_2^T $$
- 组合关系 $$ e_1 \circ r_1^H = e_2 \circ r_1^T \land e_2 \circ r_2^H = e_3 \circ r_2^T \land \\ e_1 \circ r_3^H = e_3 \circ r_e^T \\ \Rightarrow r_1^T \circ r_2^T \circ r_3^H = r_1^H \circ r_2^H \circ r_3^T $$
- 通过添加简单的约束,PairRE同样可以对子关系进行编码
- 子关系定义如下 $$ \forall h,t \in ^epsilon,(h,r_1,t) \rightarrow (h,r_2,t) $$
- 采用以下约束 $$ \frac{r_{2,i}^H}{r_{1,i}^H} = \frac{r_{2,i}^T}{r_{1,i}^T} = \alpha_i, |\alpha_i| \leq 1 $$
- 可以推导出 \begin{align*} & f_{r2}(h,t) - f_{r1}(h,t) \\ &= ||h \circ r_1^H - t \circ r_1^T || - ||h \circ r_2^H - t \circ r_2^T || \\ &= ||h \circ r_1^H - t \circ r_1^T || - ||\alpha (h \circ r_1^H - t \circ r_1^T) || \\ & \geq 0 \end{align*}
- 因此可以保证$(h,r_2,t)$更加合理