QRNN¹

Novelty

• 将RNN与CNN结合
  • 卷积层用一种不使用未来数据的masked卷积来代替LSTM中参数矩阵与上一时刻隐藏层相乘的操作。捕获过去时刻信息的同时简化了LSTM中的的操作，因为在计算过程中删除了隐藏层，仅仅使用输入数据来捕获依赖
  • 池化层使用各种门结构，例如LSTM的门结构和GRU的门结构使得梯度流稳定
• 通过上述操作简化了LSTM的计算，使其可以并行

问题和动机

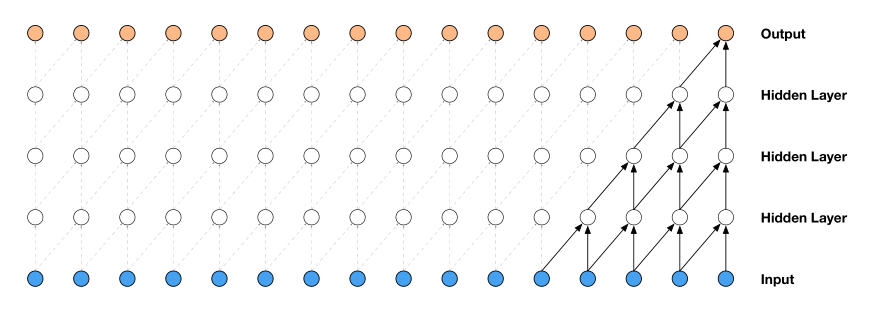
• 标准的RNN包括门变种LSTM等因为无法并行计算，因此在长序列的任务中性能受到了限制。
• 将CNN用于序列模型时
  • 并行性更好
  • 可以更好地扩展到长序列
  • 但因为最大和平均池化时假设了时间不变性，（在一次卷积池化过程中，时间步的顺序会被忽略，移动卷积核的过程中，进行相同的池化操作，不同时间步的重要性不同同样也会被忽略）因此无法充分利用大规模序列的顺序信息。
• 因此作者提出了一种将CNN和RNN混合的模型QRNN，既能跨时间步和小批量维度进行并行计算，又使得输出取决于总体顺序。性能更优秀且更节省时间

过去的解决方法

• 将CNN应用到序列模型²character-level CNN(NIPS2015)假设了时间不变性，无法利用顺序信息

  

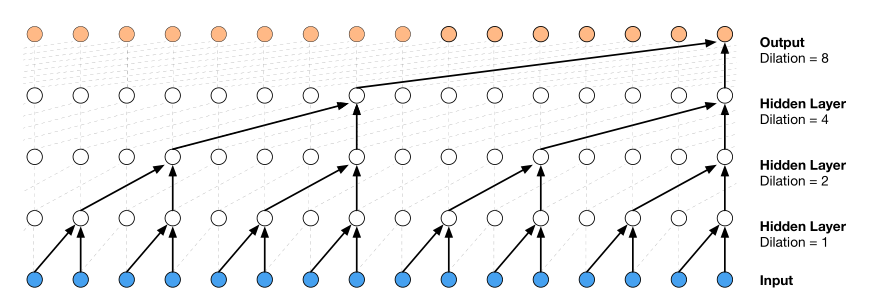
• 音频生成领域的waveNet模型³，通过五层类似于CNN的结构取得了很好效果。但这一模型在音频生成这种上一个时刻依赖很强烈的领域可能有效，但是对于NLP的其他领域并没有取得很好的效果。

  • 使用了因果卷积的假设，假设了当前时间仅仅依赖上一个时刻，但因果卷积的感受野较小，通常需要多层或者大型过滤器来增加感受野

    

  • 通过扩展卷积将感受野增大几个数量级，同时没有增加计算成本

    

• 将CNN与RNN结合⁴(待补充)

模型

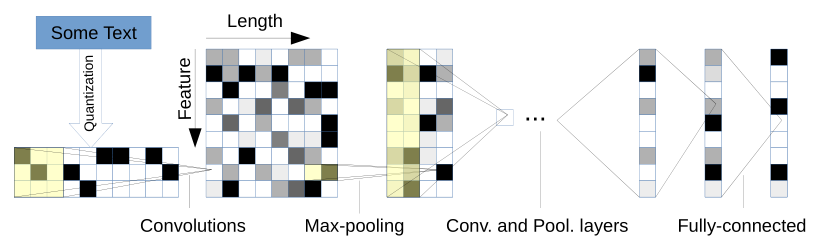
QRNN模型由两个组件构成，类似于CNN模型中的卷积层和池化层。卷积层允许在Minibatch和空间维度（顺序序列）两个层面并行化训练。池化层允许在Minibatch和特征维度两个层面并行化训练，并且池化层没有可训练的参数。

卷积组件

• 为了确保对于下一个任务的预测能力，卷积操作时不能使用未来的数据，因此使用一种masked convolution。

假设输入序列为$X \in \mathbb{R}^{T \times n}$，T为时间序列的长度，n为每个输入向量$x$的维度。$Z \in \mathbb{R}^{T \times m}$为卷积操作之后隐藏层序列，其中m为每个输入对应隐藏层的维度。卷积操作如下所示 \begin{align*} Z &= tanh(W_z * X) \\ F &= \sigma(W_f * X) \\ O &= \sigma(W_o * X) \end{align*}

其中$W_z,W_f,W_o \in \mathbb{R}^{k \times n \times m}$，k为卷积过滤器的长度，$ * $ 代表卷积操作，例如k取2时，对于每个元素而言，上述公式可写为

\begin{align*} z_t &= tanh(W^1_z x_{t-1} + W^2_z x_{t}) \\ f_t &= \sigma(W^1_f x_{t-1} + W^2_f x_{t}) \\ o_t &= \sigma(W^1_o x_{t-1} + W^2_o x_{t}) \end{align*}

• 对比LSTM中的运算
  • 可以看出去掉了隐藏层$H_t$，$z_t$代替了$\tilde{C}$，$f_t$代替了$F_t$，$o_t$代替了$O_t$

池化组件

• 对于池化组件而言，有多种选择，第一种选择仅仅使用遗忘门，第二种选择使用遗忘门和输出门，第三种选择使用遗忘门，输入们和输出门。如下所示

仅使用遗忘门 $$ h_t = f_t \odot h_{t-1} + (1 - f_t) \odot z_t $$

使用遗忘门和输出门 \begin{align*} c_t &= f_t \odot c_{t-1} + (1 - f_t) \odot z_t \\ h_t &= o_t \odot c_t \end{align*}

使用遗忘门，输入门和输出门 \begin{align*} c_t &= f_t \odot c_{t-1} + i_t \odot z_t \\ h_t &= o_t \odot c_t \end{align*}

• 与之相比，LSTM中的最后一步计算如下所示 \begin{align*} C_t &= F_t \odot C_{t-1} + I_t \odot \tilde{C}_t \\ H_t &= O_t \odot tanh(C_t) \end{align*}

变种

对于不同的任务而言可以对原始的QRNN模型进行各种改进。由于QRNN结合了CNN和RNN模型。因此对CNN和RNN模型的改进也可以应用到QRNN上。

正则化(对于RNN的改进)

• 传统的dropout方法难以在循环连接结构上产生高效的结果
• 基于变分推理的正则化(variational inference–based dropout)⁵，这种方式不适合于QRNN
• zoneout⁶

DenseNet⁷(对于CNN的改进)

• denseNet是一种在CNN模型中较为有效的连接结构,通过将层与层之间的连接二次方化，改善了梯度流和收敛性，论文的作者发现，将此连接方式用于QRNN的序列分类任务时，可以取得一定的效果提升

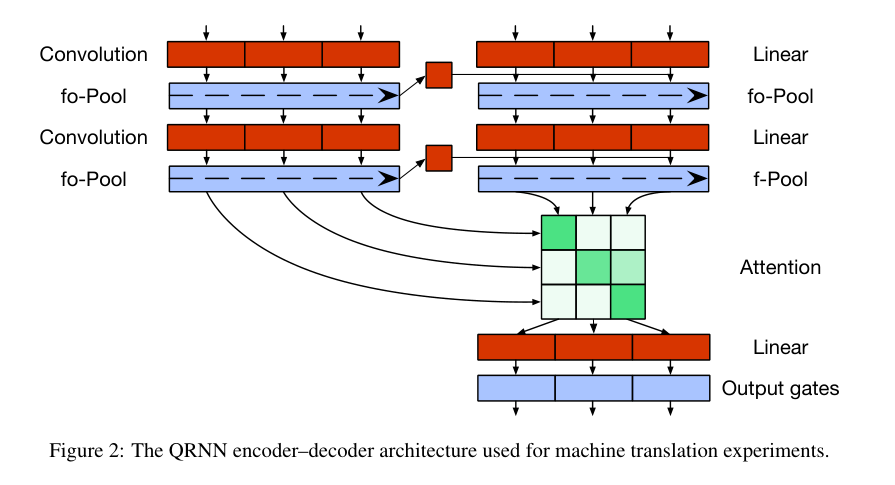
编码解码模型

• 由于传统的编码解码器结构，只是将编码器的最后一层作为解码器的第一个池化层的输入，并没有影响到解码器的卷积层，限制了模型的表现能力。
• 作者想到将编码器的最后一层状态合并到解码器的每一个时间步的卷积操作中，可以取得较好的效果。模型被修改为以下结构,其中H为编码器的最后一层隐藏层状态

我个人觉得这是实验效果不错，所以写上去的理由，引入的CNN结构或者门结构都可以捕获时序信息，只要第一个被输入到卷积层或者池化层了，后面的时间步也能获取到对应的信息。这样的改进结构类似于只有编码器对后面的层使用DenseNet连接，其实是改进了卷积层的CNN操作 \begin{align*} Z&=tanh(W_z * X + V_z * H) \\ F&=\sigma(W_f * X + V_f * H) \\ O&=\sigma(W_o * X + V_o * H) \end{align*}

• 除此之外，根据论文⁸的结果，将一个softmax卷积层放到输出前可以提升模型效果，因为不加卷积层时，仅仅是通过固定长度的向量来对所有输入进行表示。
• 在解码时引入注意力机制，具体如下
• 通过将编码器的最后一层的每一个时间步的隐藏层状态与时间步t的门操作之前的解码器状态进行内积，然后用softmax操作，得到蕴含所有时间步的编码器隐藏状态的变量$\alpha_{at}$，然后通过此变量得到注意力总和$k_t$，最后通过门操作得到$h_t^L$，卷积操作如下所示

实验

本论文在三种任务上评判了模型的性能。分别是：文档级别的情绪分类，语言模型和基于字符的神经机器翻译。