SimKGC模型

Novelty

• 使用InfoNCE损失改进原有边际排名损失，使其更专注于hard negative
• 使用IB,PB和SN三种负样本种类来增加负样本数量
• 使用图结构重排序来感知图结构

问题和动机

• 最新的基于文本（预训练模型）的方法可以访问到额外的输入信息
  • 归纳学习到训练过中看不到的实体的表示
• 但性能仍然大幅弱于基于嵌入的方法
  • 基于文本的方法中对比学习的效率过低，主要是负样本太少
  • 基于嵌入的方法不涉及昂贵的文本编码计算，因此可以使用大量负样本

同一时间 默认配置下，RotatE在Wikidata5M数据集上可以训练1000个负样本为64的epoch 基于文本的方法KEPLER只能训练30个epoch，负样本数量为1

• 因此改进现有基于文本的方法的对比学习损失，使其可以使用更多的负样本有概率提升模型的性能

相关工作

• KG-BERT使用cross-encoder架构，难以取得很好的效果(比不过基于嵌入的方法)
• 基于子图和路径挖掘的方法也比不过基于嵌入的方法

idea

• 使用的新的架构，引入新的负样本，从而增加负样本的个数
  • 采用Bi-encoder的架构，可以增大Batch，从而增大in-batch negatives的数量

  cross-encoder对于所有三元组的嵌入，需要做$e_num \times 2 \times test_num$次嵌入 bi-encoder需要做$e_num \plus 2 \times test_num$次嵌入

  • 缓存之前的batch，并作为pre-batch negatives，增加负样本数量
  • $(h,r,h)$这种类型的三元组统一作为hard negatives可以提高对比学习的性能

  因为bi-encoder，头实体关系编码$e_{hr}$与头实体编码$e_{h}$会更接近，因为相同文本更多

• 将损失从margin-based排序损失更改为InfoNCE损失，可以让模型专注于hard negatives
• 基于文本的损失关注于语义匹配而忽略了图结构信息，因此根据距离的远近进行简单的重新排序来捕获图结构信息

模型

Bi-encoder架构

• 两个编码器使用相同的预训练模型，但不共享参数(双塔模型)
• 对每个关系构建一个逆关系，即$(h,r,t) \rightarrow (t,r^{-1},h)$，因此所有的补全可以转换为尾实体的预测
• 头实体和关系的嵌入
  • 将h和r的句子描述使用一个[SEP]符号链接起来，输入到$BERT_{hr}$中，将最后一层的隐藏状态使用L2归一化的均值池化，获得关系感知嵌入$e_{hr}$
  • 即使头实体相同，但对于不同的关系可以得到不同的表示

一些文献已经指出，将bert最后一层的输出进行均值池化，效果好于使用cls处的输出

• 尾实体的嵌入与头实体和关系类似，将尾实体的描述输入到$BERT_t$中，进行l2归一化的均值池化均值池化，获得尾实体嵌入$e_{t}$
• 得分函数为余弦相似度，对于预测任务$(h,r?)$，预测结果为 $$\arg\max_{t_i}cos(e_{hr},e_{t_i}),t_i \in \mathcal{E}$$

负采样

• In-batch Negatives(IB)，同一个Batch中的三元组都属于负样本，这种策略可以复用bi-encoder模型的嵌入
• Pre-batch Negatives(PB)，取上n个参数版本的模型同一个batch的嵌入作为负样本，n通常取1或者2（MoCo有更多更新的负样本采集工作，本文没有探究）
• Self-Negatives(SN)，将$(h,r,h)$作为硬否定来增强模型性能(硬否定参考simcse)
• 模型中可能存在一种误判，正确实体有可能出现在负样本中，因此过滤掉这些实体。
• 最终的负样本数量为三者总和，假设batchsize为1024，则负样本个数为1023+nx1024+1

图结构感知

• 距离当前节点更近的节点更有可能是正确答案，因此添加一个结构感知的值 $$\arg\max_{t_i} cos(e_{hr},e_{t_i}) + \alpha \mathbb{1}(t_i \in \mathcal{E_k} (h)) $$

损失

• 采用附加margin的InfoNCE损失 \begin{align*} \mathcal{L} = -\log \frac{e^{(\phi(h,r,t)-\gamma)/\tau}} {e^{(\phi(h,r,t)-\gamma)/\tau} + \sum_{i=1}^{|\mathcal{N}|}{e^{\phi(h,r,t_i^\prime)/\tau}}} \end{align*}
• 附加margin是为了鼓励模型增加正确三元组的分数
• 温度$\tau$可以调整负样本的相对重要性，越小，越专注于硬负样本

实验

• 使用WN18RR和FB15K-237，以及Wikidata5M作为数据集来训练
• Wikidata5M含有五百万个实体和2000万个三元组，提供了两种设置，transductive，测试集中的所有实体也出现在训练集中，inductive测试集和训练集没有重合
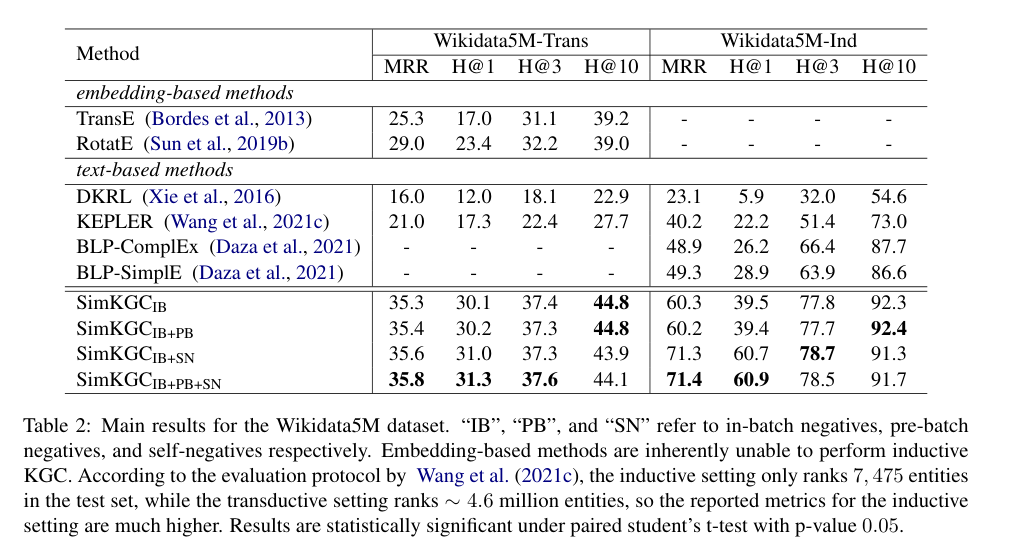
• 实验效果，在Wikidata5M上全面优于别的模型，在WN18RR上全面优于别的模型,在FB15K-237上稍有落后

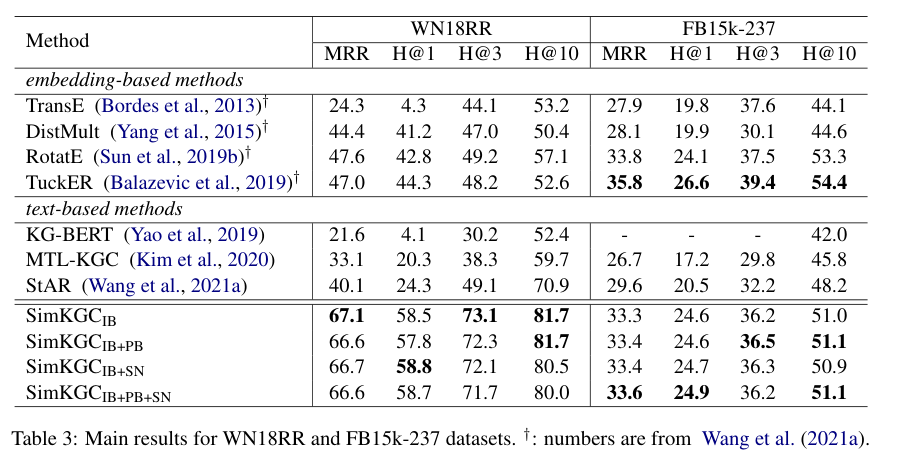
有效性分析

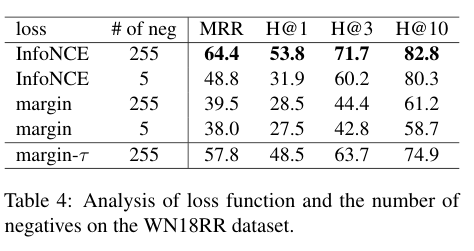
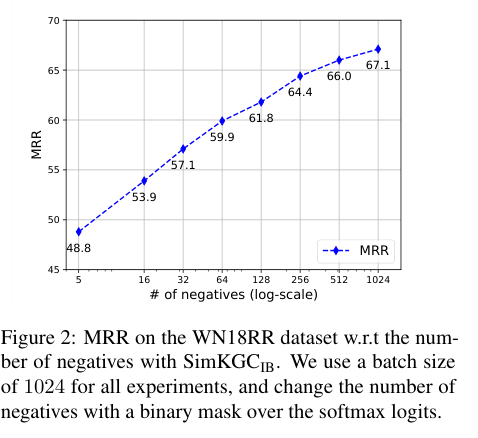
损失函数与负样本

• 模型有效可能有两个原因
  • 新的损失函数设计
  • 更多的负样本
• 改变负样本个数和损失函数，得到如下结果

  

• 可以看出二者皆有一定的影响，但损失函数的影响似乎更大，InfoNCE中，硬负样本会产生更大的梯度，添加更多的负样本可以产生更稳健的表示。硬度感知特性对于对比损失的成功至关重要
• 同时提出了一个变种$margin-\tau$损失，通过改变margin损失前面的1/N，将其转换为$\frac{\exp(s(t^\prime_i)/\tau)}{\sum_{j=1}^{|\mathcal{N}|}\exp(s(t^\prime_j)/\tau)}$，其中$s(t^\prime_i) = \max(0, \lambda + \phi(h,r,t^\prime_i) - \phi(h,r,t))$
• 与InfoNCE相似,$margin-\tau$可以更多的关注硬负样本，从而得到更高的性能提升，这与RotatE中的自对抗负采样类似。

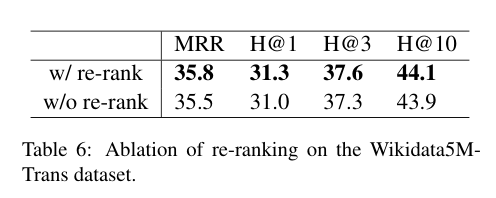
图结构重排序

• 通过重排序，性能会有一定的提升，但重排序并不总是通用的，未来可以考虑使用图神经网络的方式来实现更高效的图结构感知

改进方向

• 探索更有效的损失
• 对多种模式和复杂关系的建模(预测一对N时，N的一端性能不佳，可能由于语义上很多答案都是对的，但知识图谱不完整)
• 采用更高效的方式来捕获图结构(导致FB15k-237表现不佳)